Overview

Introduction

radioactivedecay is a Python package for radioactive decay calculations. It contains functions to define inventories of radionuclides, perform decay calculations, and output decay data for radionuclides and decay chains.

The original goal was to create a light-weight Python package for radioactive decay calculations, with full support for branching decays, multi-step decay chains, and metastable states. By default radioactivedecay uses decay data from ICRP Publication 107 [1] and atomic mass data from the Atomic Mass Data Center (AME2020 and Nubase 2020 evaluations) [2], [3] and [4]. It solves the radioactive decay differential equations analytically using basic linear algebra operations [5].

In order to use radioactivedecay, you will need Python 3.8+ with the Matplotlib, NetworkX, NumPy, Pandas, SciPy, Setuptools and SymPy packages installed. The code is platform independent and has been tested on Windows, MacOS and Linux systems.

Quick start

Install radioactivedecay using pip by:

$ pip install radioactivedecay

or using conda by:

$ conda install -c conda-forge radioactivedecay

Either command will attempt to install the dependencies (Matplotlib, NetworkX, NumPy, Pandas, SciPy, Setuptooks & SymPy) if they are not already present in the environment.

Import the radioactivedecay package and decay a simple inventory using:

>>> import radioactivedecay as rd
>>> inv_t0 = rd.Inventory({'H-3': 10.0}, 'Bq')
>>> inv_t1 = inv_t0.decay(12.32, 'y')
>>> inv_t1.activities()
{'H-3': 5.0}

Here we created an inventory of 10.0 Bq of tritium (³H) and decayed it for 12.32 years. The activity reduced by a factor of two, i.e. to 5.0 Bq, as 12.32 years is the half-life of tritium.

Additional options for inputs and outputs include masses, moles and numbers of atoms. Use the units argument to the Inventory() constructor, and the masses(), moles(), numbers(), mass_fractions(), and mole_fractions() methods to obtain results.

>>> inv_mass_t0 = rd.Inventory({'H-3': 3.2}, 'g')
>>> inv_mass_t1 = inv_mass_t0.decay(12.32, 'y')
>>> inv_mass_t1.masses('g')
{'H-3': 1.6000000000000003, 'He-3': 1.5999894116584246}

>>> inv_mol_t0 = rd.Inventory({'C-14': 1.0}, 'mol')
>>> inv_mol_t1 = inv_mol_t0.decay(3000.0, 'y')
>>> inv_mol_t1.moles('mol')
{'C-14': 0.6943255713073281, 'N-14': 0.3056744286926719}
>>> inv_mol_t1.numbers()
{'C-14': 4.181326323680147e+23, 'N-14': 1.840814436319853e+23}
>>> inv_mol_t1.mole_fractions()
{'C-14': 0.6943255713073281, 'N-14': 0.3056744286926719}

Use the plot() method to show the decay of the inventory over time:

>>> inv_t0.plot(100, 'y')

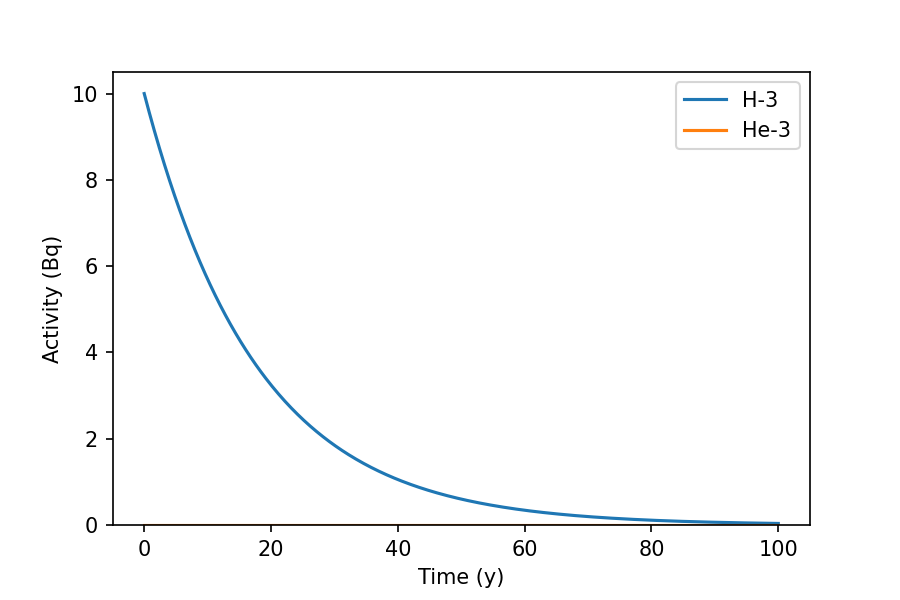
The graph shows the decay of H-3 over a 100 year period.

Use the Nuclide class to fetch decay and atomic data about a particular nuclide and to draw diagrams of its decay chain:

>>> nuc = rd.Nuclide('H-3')
>>> nuc.half_life('readable')
'12.32 y'
>>> nuc.progeny()
['He-3']
>>> nuc.decay_modes()
['β-']
>>> nuc.branching_fractions()
[1.0]
>>> nuc.Z  # proton number
1
>>> nuc.A  # nucleon number
3
>>> nuc.atomic_mass  # atomic mass in g/mol
3.01604928132
>>> nuc.plot()

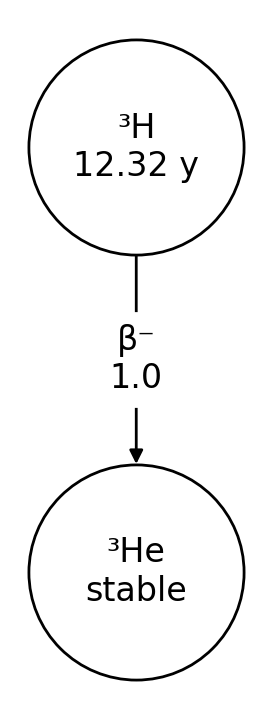
How it works

radioactivedecay calculates an analytical solution to the decay chain differential equations using matrix and vector multiplications. It implements the method described in ref. [5]. See the theory docpage for more details. It calls NumPy [6] and SciPy [7] for the matrix operations. There is also a high numerical precision decay calculation mode based on SymPy [8] routines. Decay time series data can be output as a Pandas [9] dataframes.

The datasets repo on GitHub contains a Jupyter Notebook for creating the ICRP-107 decay dataset. Notebooks with cross-checks of decay calculation results against PyNE [10] and Radiological Toolbox [11] are held in the comparisons repo.

Limitations

At present radioactivedecay has the following limitations:

• It does not model neutronics, so cannot calculate radioactivity produced from neutron-nuclear reactions inducing radioactivity or fission.

• It cannot model temporal sources of external radioactivity input or removal from an inventory over time.

• Care is needed when decaying backwards in time, i.e. supplying a negative argument to the Inventory.decay() method, as this can result in numerical instabilities and nonsensical results. The high precision InventoryHP.decay() is more robust to these instabilities, but not immune from them.

There are also some limitations associated with the ICRP-107 decay dataset:

• ICRP-107 does not contain data on branching fractions for radionuclides produced from spontaneous fission decays. Thus the decay() methods do not calculate activities for spontaneous fission progeny.

• Decay data is quoted in ICRP-107 with up to 5 significant figures of precision. The results of decay calculations will therefore in theory never be more precise than this level of precision.

• Uncertainties are not quoted for the radioactive decay data in ICRP-107. Uncertainties will vary substantially between radionuclides. They will depend on how well each radionuclide has been researched in the past. In many cases these uncertainties will be more significant for the results of decay calculations than the previous point about the quoted precision of the ICRP-107 decay data.

• There are a few instances where minor decay pathways were not included in ICRP-107, e.g. the decay pathways for At-219-> Rn-219 (β ~3%), Es-250 -> Bk-246 (α ~1.5%), and U-228 -> Pa-228 (ε ~2.5%). For more details see refs. [12] and [13] on the creation of the ICRP-107 dataset.

License

radioactivedecay is open source software released under the MIT licence.

The default decay data used by radioactivedecay is ICRP-107 [1], which is Copyright © A. Endo and K.F. Eckerman (2008). See LICENSE.ICRP-07 for more details.

The default atomic mass data is based on the Atomic Mass Data Center (AMDC) AME2020 [2], [3] and Nubase2020 [4] evaluations. See LICENSE.AMDC for more details.

Citation

If you find this package useful for your research, please consider citing the paper on radioactivedecay published in the Journal of Open Source Software:

A. Malins & T. Lemoine, radioactivedecay: A Python package for radioactive decay calculations. Journal of Open Source Software, 7 (71), 3318 (2022). DOI: 10.21105/joss.03318.

Contributors

List of contributors to radioactivedecay:

• Alex Malins

• Thom Lemoine

• Bernardo Gameiro

• Ian Cullen

Contributing

Users are welcome to fix bugs, add new features or make feature requests. Please read the contributor guidelines and open a pull request or issue on the GitHub repository.

Queries and suggestions

If you have any questions or suggestions, please post on the Discussions page on GitHub.

Acknowledgements

Special thanks to:

• Center for Computational Science & e-Systems, JAEA

• Kenny McKee

• Daniel Jewell

• Ezequiel Pássaro

• Kelly Rowland

• Shyam Dwaraknath

• Madicken Munk

• Kristen Thyng

• Wolfgang Kerzendorf

• Hunter Ratliff

• Jayson Vavrek

• Jonathan Wing

• @radioactivedecay-github

• Christian Schreinemachers

• Sean Neutzmann

• @buresjan

for suggestions, support and assistance to this project.

Thanks also to:

• Björn Dahlgren (creator of the batemaneq Python package [14])

• Anthony Scopatz and the PyNE project [9]

• Jonathan Morrell (creator of the NPAT and Curie packages)

• Austin Ladshaw & collaborators (creators of IBIS [15])

• Will Johnson & collaborators (creators of SandiaDecay)

for their work on open source radioactive decay calculation software.

References

1. ICRP Publication 107: Nuclear Decay Data for Dosimetric Calculations. Ann. ICRP 38 (3), 1-96 (2008). PDF

2. WJ Huang et al. Chinese Phys. C 45, 030002 (2021). DOI: 10.1088/1674-1137/abddb0

3. Meng Wang et al. Chinese Phys. C 45, 030003 (2021). DOI: 10.1088/1674-1137/abddaf

4. FG Kondev et al. Chinese Phys. C 45, 030001 (2021). DOI: 10.1088/1674-1137/abddae

5. M Amaku, PR Pascholati & VR Vanin, Comput. Phys. Comm. 181, 21-23 (2010). DOI: 10.1016/j.cpc.2009.08.011

6. CR Harris et al. Nat. 585, 357-362 (2020). DOI: 10.1038/s41586-020-2649-2

7. P Virtanen et al. Nat. Methods 17, 261-272 (2020). DOI: 10.1038/s41592-019-0686-2

8. A Meurer et al. PeerJ Comp. Sci. 3, e103 (2017). DOI: 10.7717/peerj-cs.103

9. The pandas development team (2020). DOI: 10.5281/zenodo.3509134

10. PyNE: The Nuclear Engineering Toolkit. https://pyne.io/

11. KF Eckerman, AL Sjoreen & C Sun, Radiological Toolbox, Oak Ridge National Laboratory. https://www.ornl.gov/crpk/software

12. A Endo, Y Yamaguchi & KF Eckerman, JAERI 1347 (2005). DOI: 10.11484/jaeri-1347

13. A Endo & KF Eckerman, JAEA-Data/Code 2007-021 (2007). DOI: 10.11484/jaea-data-code-2007-021

14. B Dahlgren, batemaneq: a C++ implementation of the Bateman equation, and a Python binding thereof. https://github.com/bjodah/batemaneq

15. A Ladshaw et al. Comput. Phys. Comm. 246, 106907 (2020). DOI: 10.1016/j.cpc.2019.106907